Arithmetic Tricks - Difference of two
There is a neat trick when multiplying two numbers that are very close to each other, specifically by a difference of two; for example, 13 × 11.
The trick is this - if the numbers differ by 2, take the number in between, square it, and subtract 1.
So 13 × 11 = 12² - 1 = 144 - 1 = 143
Here’s why
Imagine a square of side length ‘n’. It has area n².
The original square
If we draw lines, a distance of ‘1’ from the right and bottom, we create four sections. One is a square of side length (n-1), we have two rectangles of sides 1 and (n-1) and we have a unit square of side length 1.
Dividing the square
If we take the bottom rectangle, this has an area of 1 × (n - 1).
This rectangle has area 1 × (n - 1)
We can move this rectangle and bolt it onto the right end of our diagram.
Move the rectangle
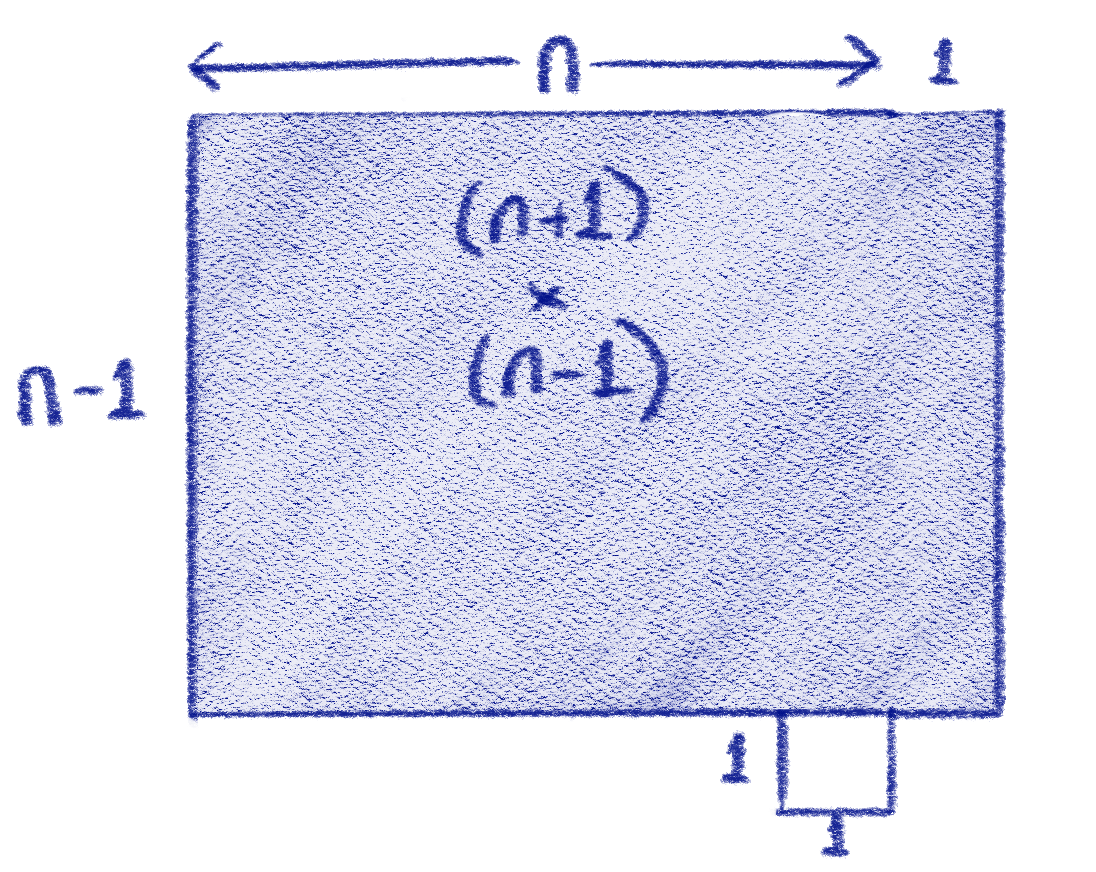
We now have a new rectangle, with sides (n-1) and (n+1), with a square left over.
We have a new rectangle and a square left over
The total area of this shape is the same as the original.
Thus n² = (n-1) × (n+1) +1
or (n-1) × (n+1) = n² -1
This is why the trick works. 11 × 13 = 12² - 1
Generalising
We can use the same method for any two numbers, instead of shaving off a width of ‘1’, we shave off whatever is needed to get to the halfway point between the two numbers
(n-a) × (n+a) = n² - a²
If you have done any maths, you will probably know that this is the ‘difference of two squares’.
So, 13 × 17 = 15² - 2² = 225 - 4 = 221
Caveat
The thing with the ‘methods you learn at school’ is they are reliable, they always work. Mental arithmetic tricks sometimes provide a shortcut, sometimes they’re making life more difficult. They are tools that only help in certain situations, and the skill is recognising when you have such a situation and the flexibility to take advantage.
For example, 2 × 3 = 2.5² - 0.5² is not very useful!
However, this does give us a new trick.
What if we want 2.5²?
We note that n² = (n-a) × (n+a) + a²
So, setting a=0.5,
2.5² = 2 × 3 + ½² = 6 + ¼ = 6.25
2.5² = 6.25
Recent Arithmetic Posts
More Maths Posts